Introduction

Oh the fun we get out of running the following in Shapely, do we know what’s going under the hood?.

p3 = p1.intersects(p2)
p4 = p1.union(p2)

I’m not “guilt-trip"ing you, haha! If you’re still down, here are some things I learnt while diving deeper into geometry operations in GIS libraries.

Approach

I had a simple task at hand, to go through shapely’s codebase and identify how vector geometry algorithms are implemented.

While I have seen GEOS mentioned here and there in wider Geospatial GitHub, and have used Shapely moderately extensively, I’ve never read the first few lines of Shapely docs. It clearly mentions that it’s a port of GEOS. I often dig into abstractions in modern software engineering / software environment threads on Twitter, so all of them came scaringly knocking at my door when I learnt that GEOS is a port of JTS.

I tried hard to navigate through a library which powers most geospatial vector ops running in your computers, (yes, including Turf.js). I still haven’t found my way, I’m lost here, feel free to help here.

An alternate path to glory

Now then, since I’ve got your hopes up, allow me to enlighten you of high-school geometry. Let’s dissect some common geomrtric operations on vectors. Here on, by Geometry I mean a Point, LineString, Polygon. We can extend the discussion for MultiLineString, MultiPoint.

within

A boolean operation on a couple of geometries as described here.

• a Point within a Point is an equality operator
• a Point(p1) within a LineString(l1) is iterating through the line segments defined in l1 and check if p1 lies in one of the segments.
• a Point(p1) within a Polygon can be calculated by Ray-casting. It can also be calculated by calculating the sum of angles subtended by each side of the polygon to the point, it’s also mentioned here and graphically explained here. We’ll be referring to this point often, so let’s refer to this explanation as t1.
• a LineString(l1) within another LineString(l2) can be calculated by checking if all “defined line segments” make at least one 0 degree with the line “defined line segments” of l2.
• a LineString(l) within a Polygon(p) can be calculated by checking if all “defined points” in l are inside p.
• a Polygon(p1) inside another Polygon(p2), can be calculated by checking if all “defined points” in p1 are inside p2.

We can invert the results to check if a geometry is outside another.

union and intersection

A boolean operation on a couple of geometries as described here.

For convex polygons, a barebone solution can be modelled as follows. In the diagrams below, we can find the area of intersection in the following way.

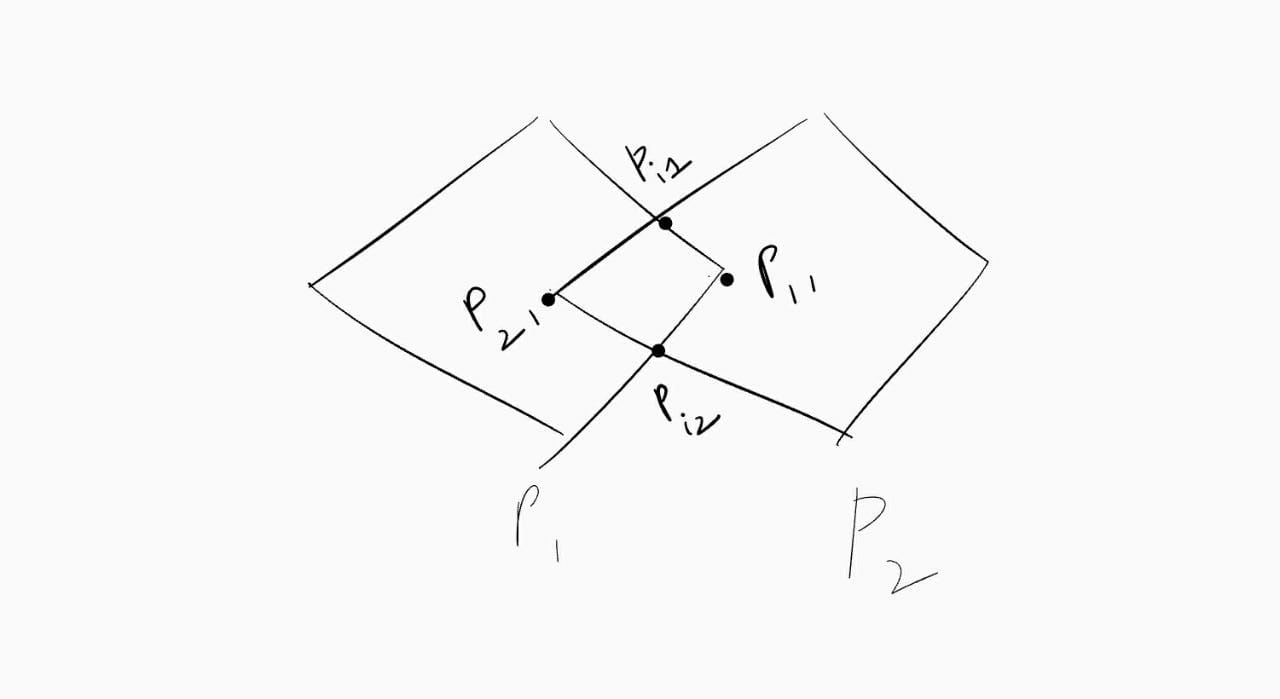
1. For both polygons we find vertices which lie inside the other polygon - P11, P21
2. We find the intersection points of these polygons - Pi1, Pi2
3. Order them in a cyclic manner (Take centroid and measure angles against a direction, and sort them based on the angles?)

If one looks at the diagrams closely, they can see it more clearly that we can find the union of convex polygons if we find vertices which lie outside the other polygon.

Of course this has a greater time complexity and I’m sure they are implemented differently under the hood, but hey, something to start with!

Geospatial indices and how can give you glory faster!

Most of us know about indexing in a generic database, how we structure data at an extra cost while writing, and make reads faster by optimizing on where to look the data for in memory/disk.

Geospatial indices work in a similar fashion, for instance if a query asks if a point falls in 100 polygons, indexing should ideally help us make it faster than an O(n) * (time to query if a point lies in a polygon).

Here’s how R-tree indexing works, the most intuitive spatial indexing algorithm. This can also be extended to 3, 4 dimensions.

• Let’s say we have polygon A, let’s act like apes and draw a rectangular grid tangentially around it, let’s call it R(A).

• Now if we get a contains query for polygon A and a point P, if R(A) doesn’t intersect with P, A definitely doesn’t.

• Similarly let’s call bounding rectangles of B, C, D, E, F as R(B), R(C), R(D), R(E), R(F) respectively.

•  A has C, D, B has E
  

• Clearly D is within C, which is within A and their MBRs - minimum bounding rectangles as well respectively. If something is within D or F, it’s within C and A. One can imagine a tree forming like this.

  A----B
  |    |
  C-   E
  | |
  D F
  

Searching if a point falls within F just got a tiny bit faster. In a real-life spatial database, a R-tree looks like this, and queries are generally n*X faster.

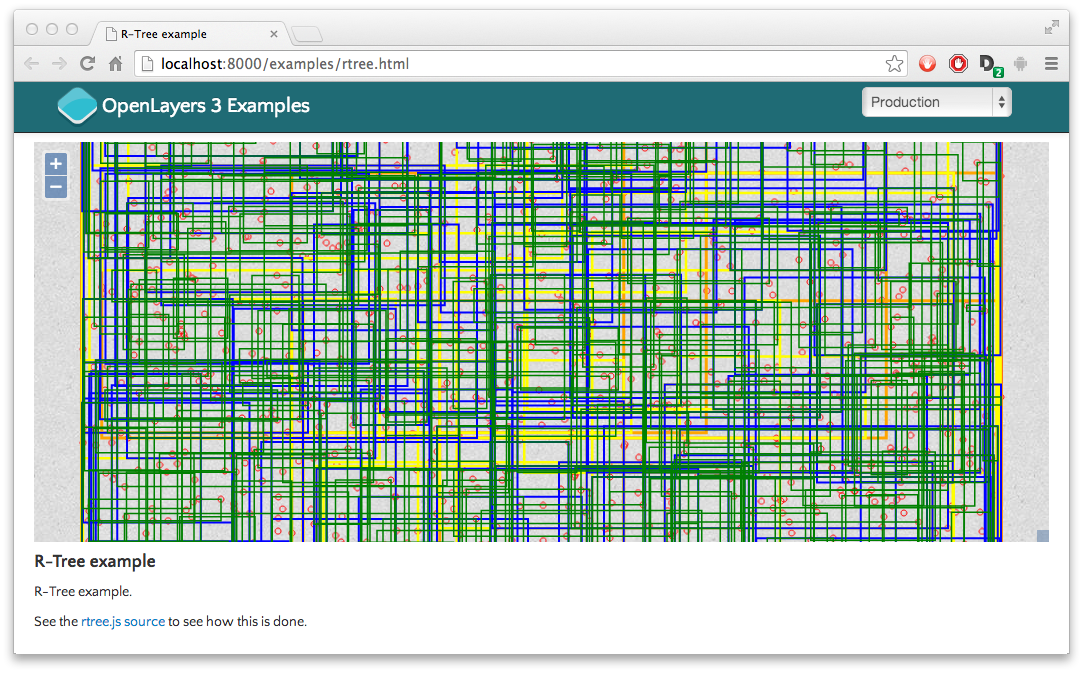
Some other kinds of indexing are

• some variants of R tree like R* tree, with different splitting heuristics(if a node has many child nodes so that it becomes a blocker for performance, it can be split)
• Quadtrees and derivatives.
• Generic grid indices like H3, S2
• Space filling indices like like Hilbert Curves, or Z curves.

Hope this leaves you with something to think about, good day!